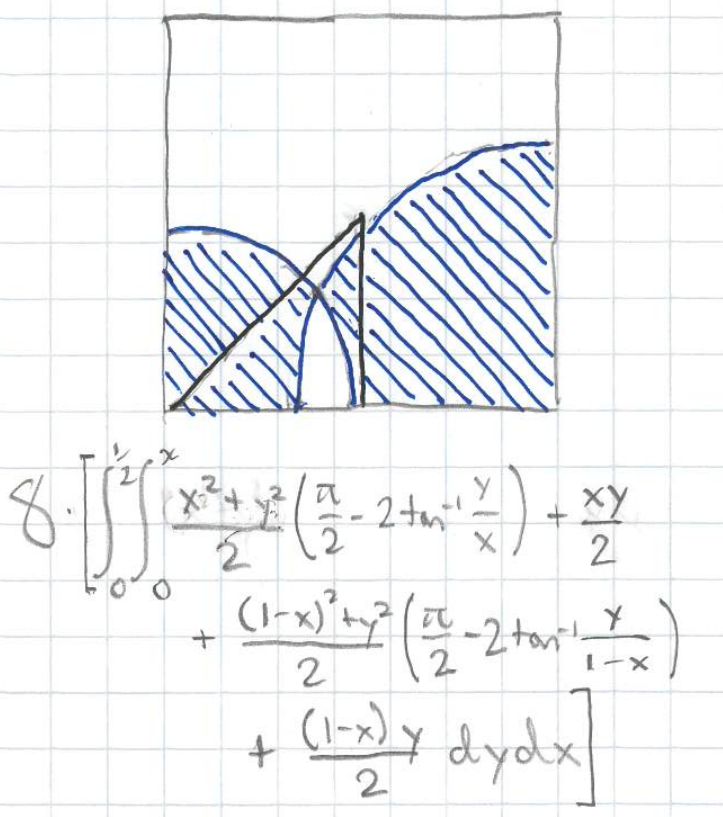
For our November puzzle you had to compute the probability that two ordered points, randomly uniformly selected from a square, would have an equidistant point on the edge closest to the first point in the pair. Given the first point, without loss of generality uniformly selected from a lower triangular octant of the square outlined in black above, the second point would need to be in the blue-shaded symmetric difference of two circles centered at the bottom vertices of the square that pass through the first point.

The precision requested for the answer meant an analytical solution likely would be required. Below the diagram is an integral expressing the total area of these blue-shaded regions, which comes to (1 + 2π - ln(4))/12, or approximately 0.4914075788…

Congrats to the November solvers that computed the tricky probability!