Beside the Point
November 2024 : Puzzle
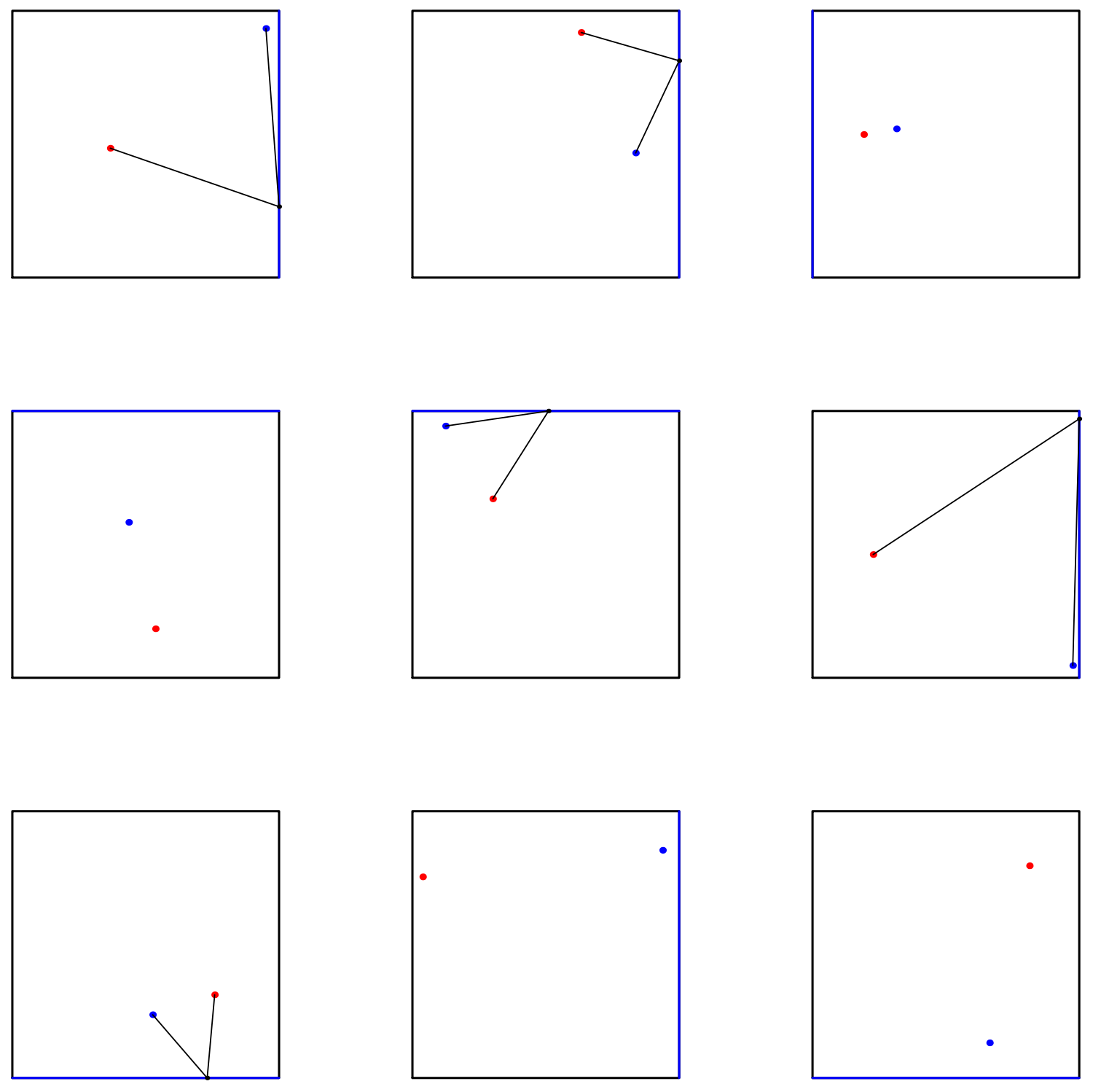
Two random points, one red and one blue, are chosen uniformly and independently from the interior of a square. To ten decimal places1, what is the probability that there exists a point on the side of the square closest to the blue point that is equidistant to both the blue point and the red point?
-
(Or, if you want to send in the exact answer, that’s fine too!) ↩