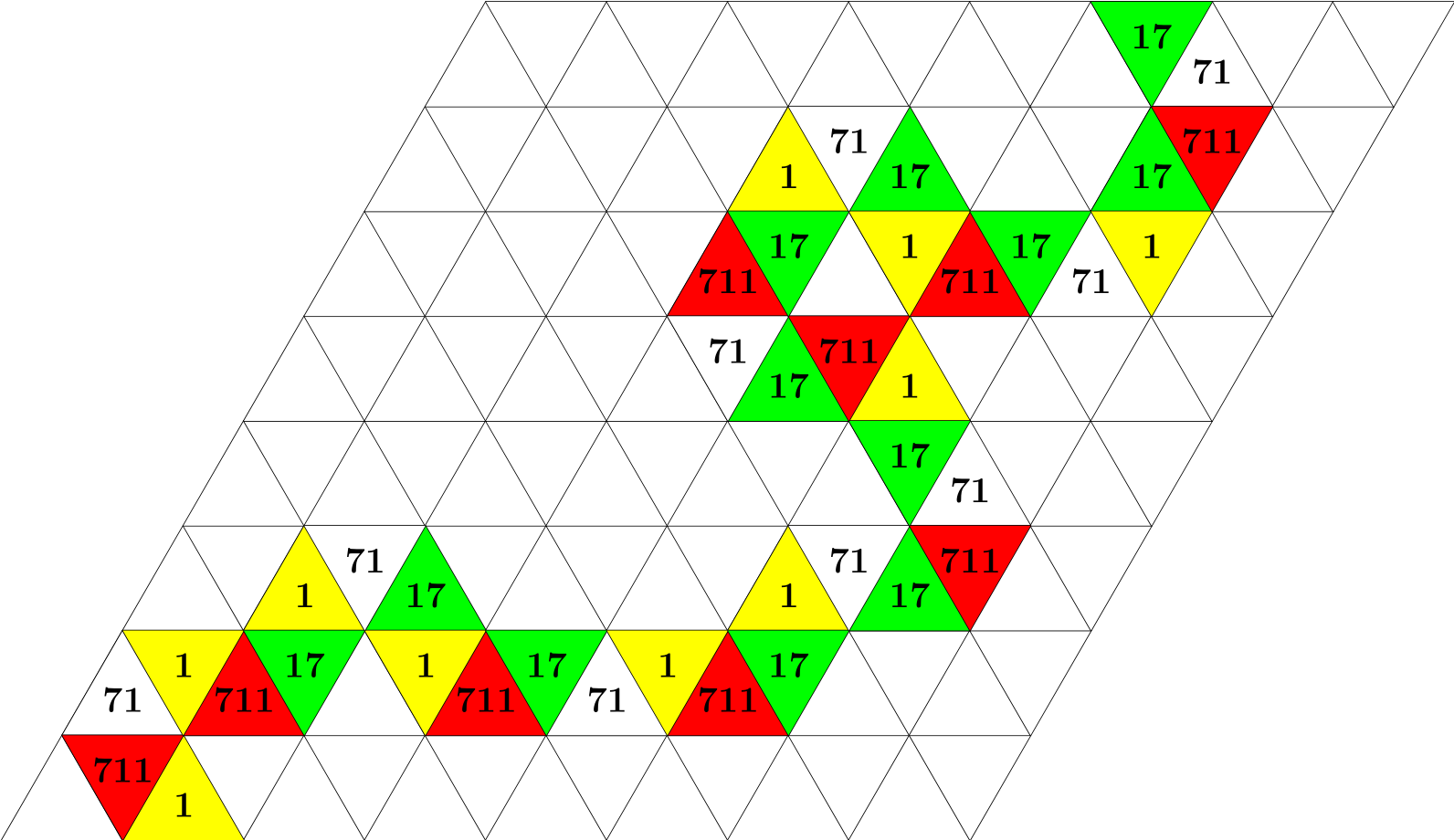
As it turns out there are very few paths the tetrahedron can take from top to bottom, and the shortest/cheapest one is presented here. The sum of the numbers the tetrahedron rolls over on its path is 7252.

Astute solvers noticed that for a tetrahedron with sides A, B, C, and D, when it rolls in a “straight line” (such as moves 2 thru 5 in this solution), the faces on the paper form the pattern ABCDABCD…, and when it begins to roll in a “circle” (such as the one begun by moves 1 thru 4 in this solution), the faces on the paper form the pattern ABCABCABC… . From there, one can logically deduce the path the tetrahedron must take.

Congratulations to everyone who solved this month’s puzzle!