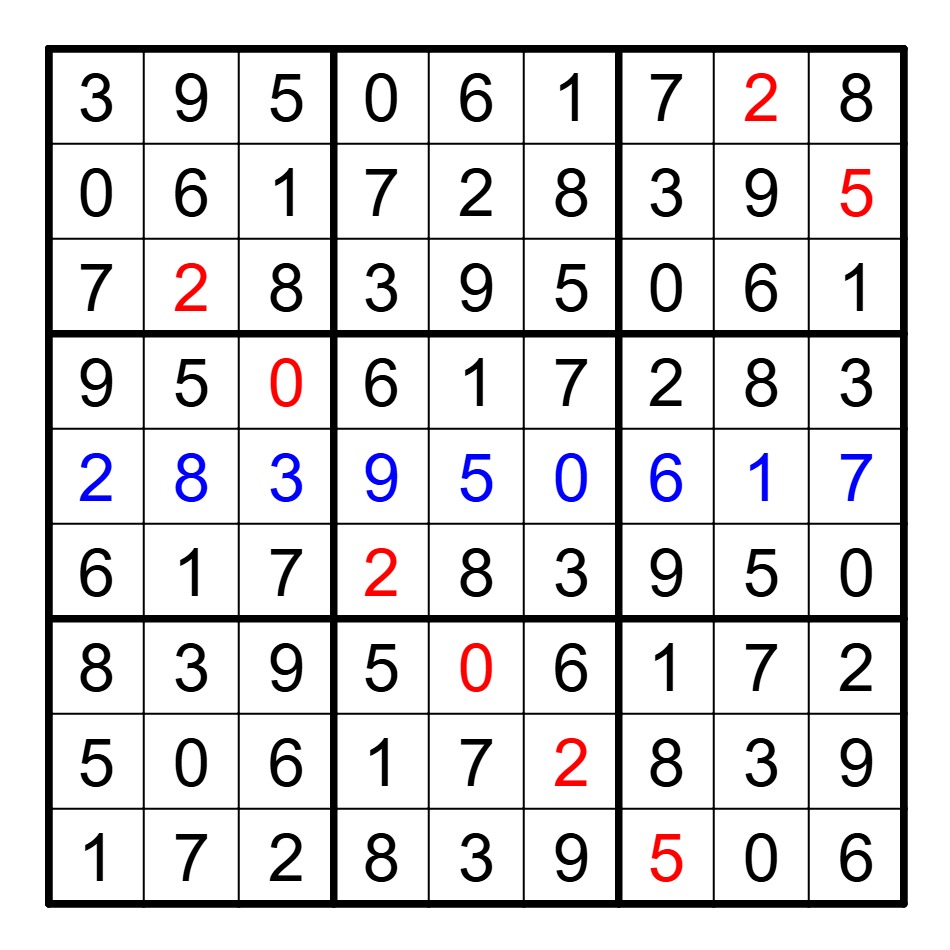
There are a few ways one could go about this month’s puzzle. Many of you took a purely code-based approach, and were able to find the board above.

But a number-theory approach also works. Let S be the sum of the digits in the first row, and let d be the GCD of the 9-digit numbers formed by the nine rows. The sum of these 9-digit numbers will be 111,111,111×S = 3×3×37×333,667×S, and so d must be a divisor of this value. (Furthermore, if a 9-digit integer N is a divisor of 999,999,999, then any cyclic permutation of N will be as well¹.)

We know our rows all contain 0, 2, and 5. One of them begins with a 0, so let’s look at large divisors of 111,111,111 to see if mutliples of any of them are 8-digit numbers with distinct positive digits and which contain a 2 and a 5. It turns out 37×333,667 = 12,345,679 is one such number. The only other 8-digit multiples of 12,345,679 with distinct positive digits are 24,691,358, 49,382,716, and 61,728,395. This last value, when cyclically shifted 8 times, is the one that can validly populate the sudoku grid. The 9-digit number formed by the unclued middle row is 283,950,617, the answer to this month’s puzzle.

Congrats to the January solvers for finding the optimizing grid!