Aaron has learned that Erin always plays a fixed distance — call it e — along the correct angle. Erin knows that Aaron knows this, and that Aaron will pick a distance a (and an angle at random, presumably) to maximize P(Aaron wins). So Erin should pick a value for e that minimizes this probability.

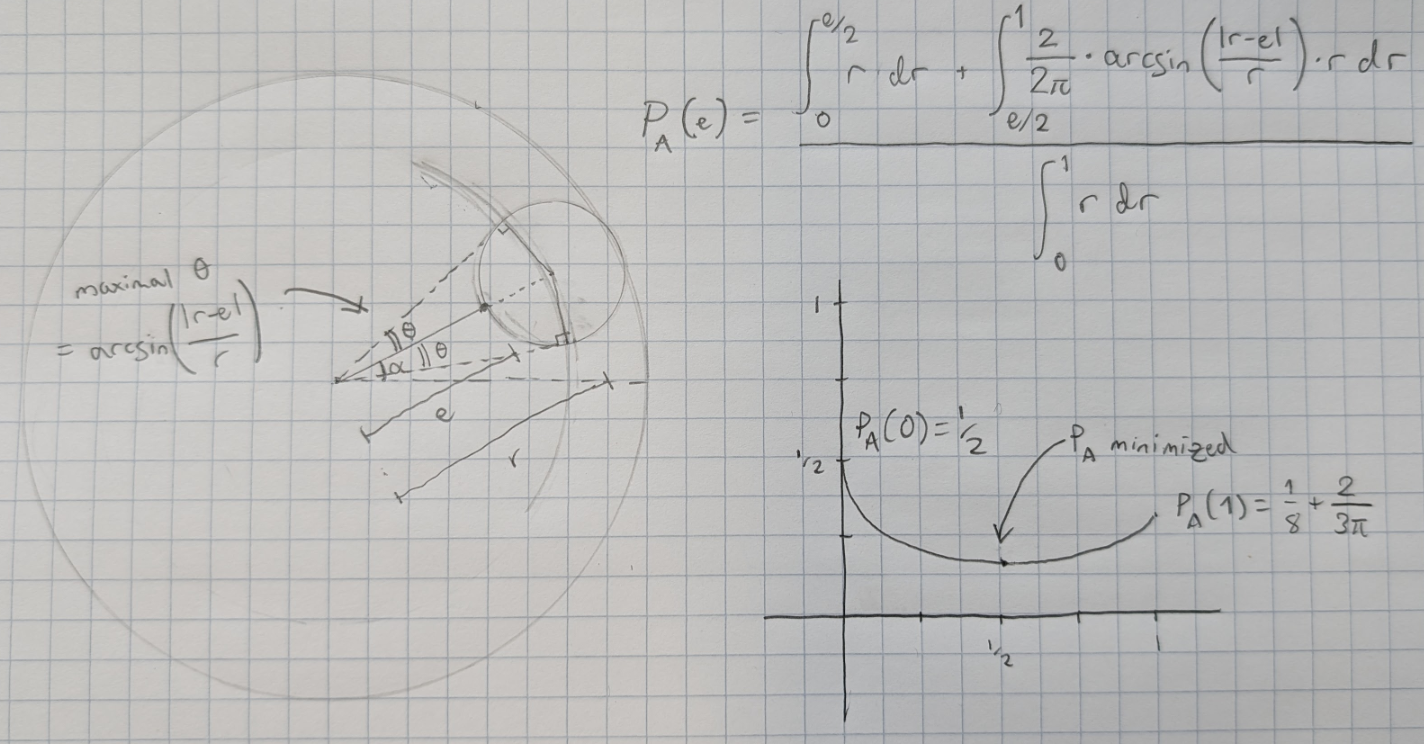
So we need to determine P(Aaron wins) for given values of e and r. If r is less than e/2, Aaron should choose to stay at the center, thus guaranteeing a win. Otherwise, Aaron should pick the distance a that maximizes the fraction of the circle of radius a located within a distance of |r−e| of the flag.

Maximizing the fraction of the circle of radius a inside the radius-|r−e| circle is equivalent to maximizing the subtended angle determined by the circles’ intersection points. This gives rise to the arcsin integral above. (The r multiplier inside both integrals and 2 multiplier generated by the bottom integral is to account for polar coordinates — e.g. if the flag has an ε probability of being placed in a tiny annulus of radius ≈δ, it has a 2ε probability of being placed in a tiny annulus of radius ≈2δ.)

Numerically solving for the e that minimizes the probability above gives e ≈ 0.501306994212753; plugging that into the integral above gives P(Aaron wins) ≈ 0.166186486474004.

Congrats to this month’s solvers!