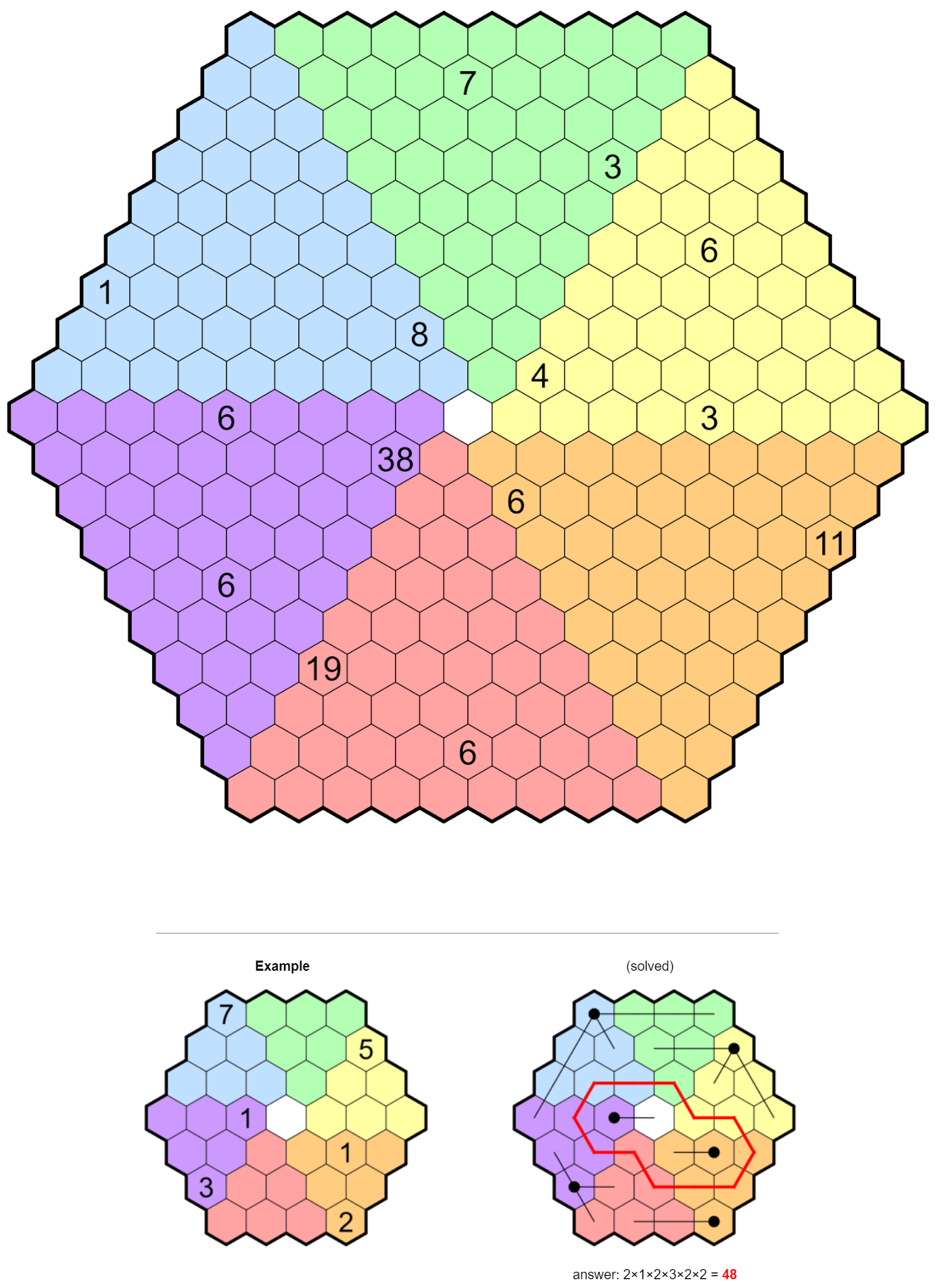
A field is divided into hexagonal cells of width 1. Some of the cells contain “posts” at their center. Each post is represented in the field (grid) by a number. Construct one or more fences emanating from each post, such that the total length of fence connected to a post equals the number given. Fences are straight line segments with integer length and can only intersect cell walls at right angles. Fences from different posts may not touch, nor may a fence from one post touch a different post.

The goal of this puzzle is to build your fences in such a manner that it is possible to draw a closed loop through some of the remaining empty cells. The loop may only make 120-degree turns, and it must visit each of the six colored regions. Finally, the loop must be symmetric in some way (either via rotation or reflection).

As in the example, the loop must be rectilinear, passing through the centers of adjacent empty cells.

Once you have completed the loop, determine the number of cells it visits in each of the six colored regions. The answer to this month’s puzzle is the product of these six values.