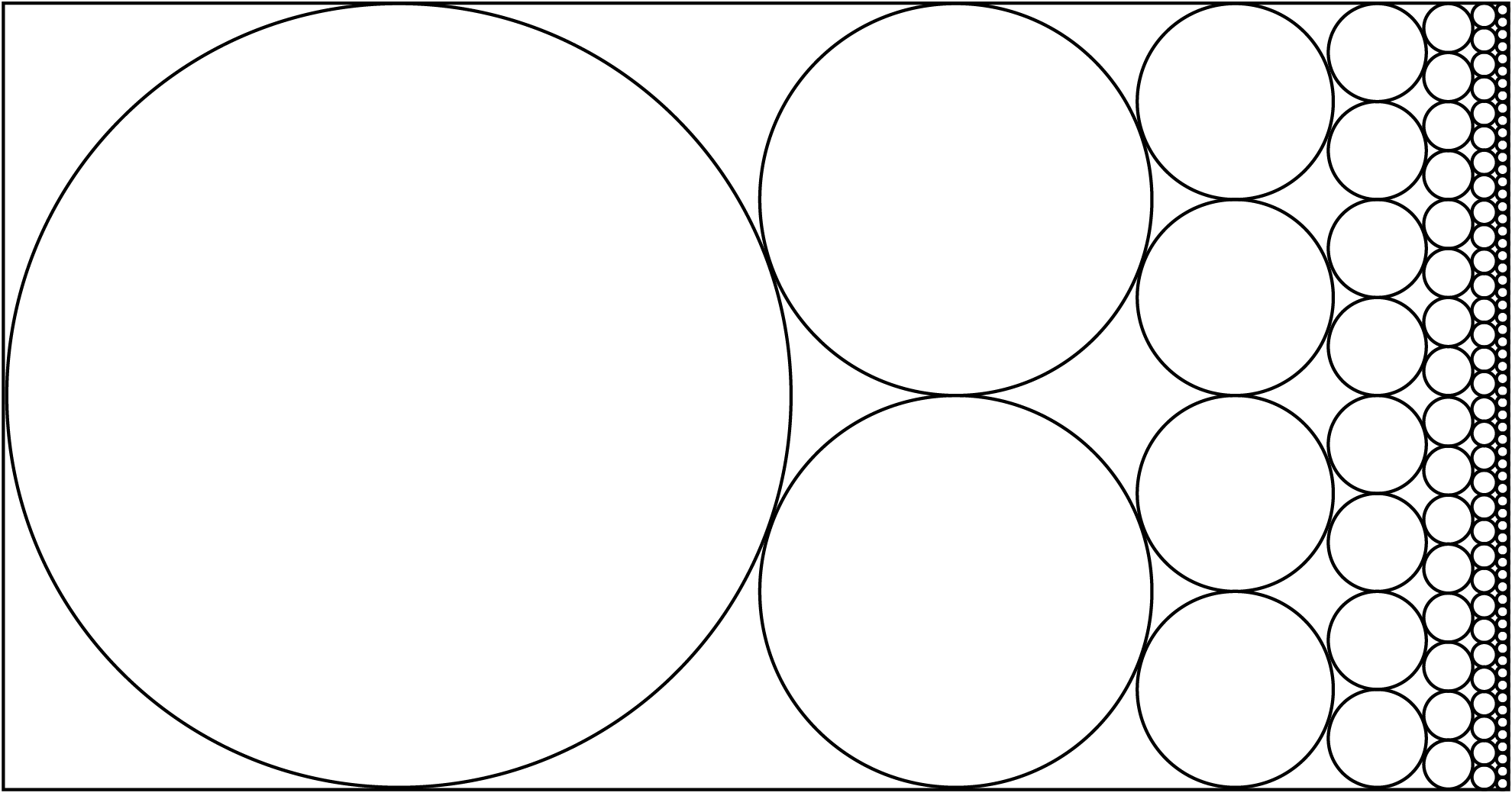
Each stack of circles has twice as many circles as the stack to its left, with each circle having half the radius as those in the stack to its left, and there are infinitely many such stacks. Every circle touches another circle or the rectangle at exactly 5 points, and the rectangle is just wide enough to hold all the circles. What proportion of the rectangle is covered by a circle?

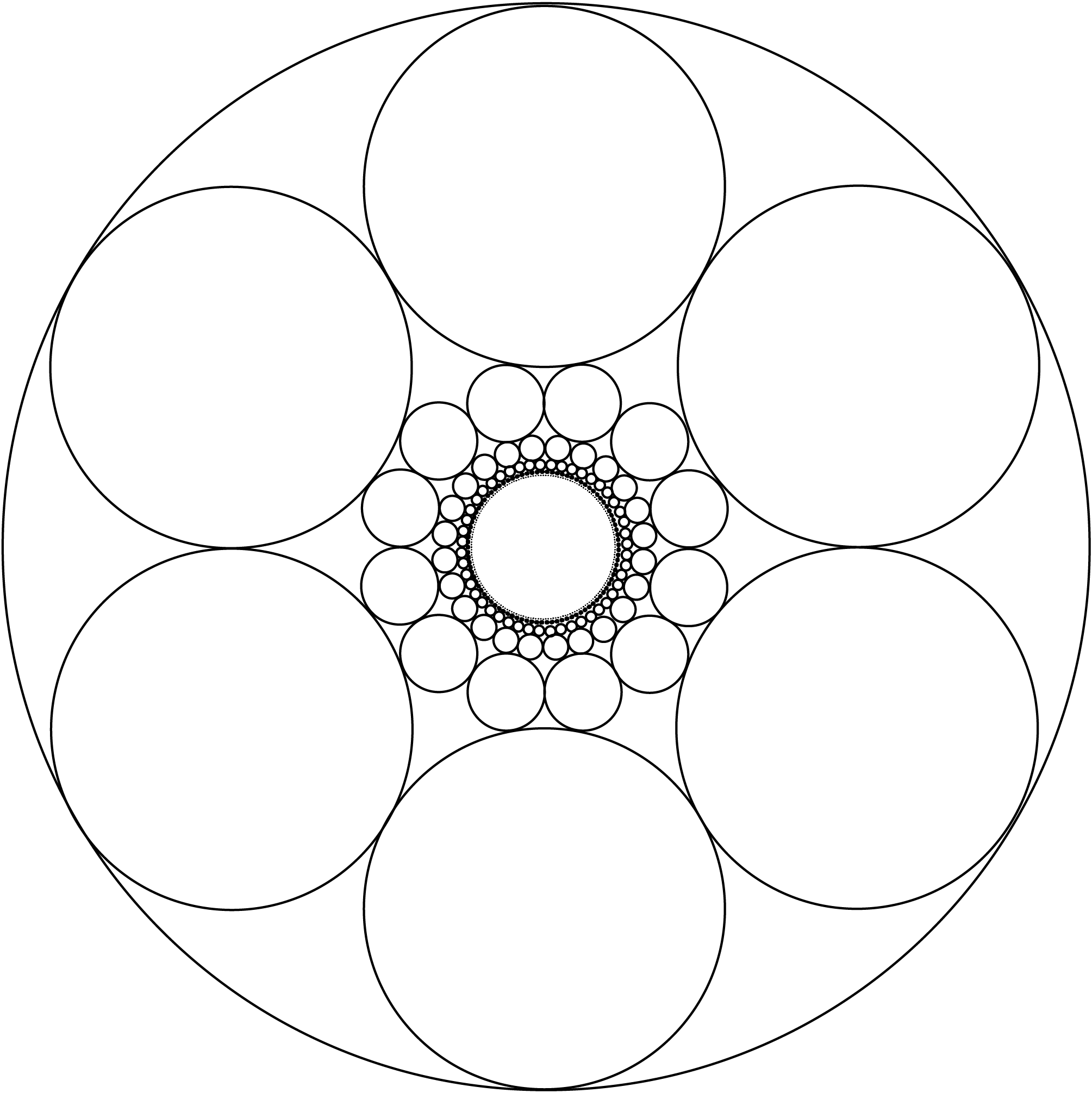This large circle, of radius 1, contains infinitely many rings of circles. Each ring contains a collection of equally sized circles that are tangent to their two neighbors in the ring and are all equidistant from the center of the large circle. The outermost ring, containing six circles, is tangent to the large circle at six places. Every subsequent ring has twice as many circles as the previous ring, and every circle in the ring is tangent to exactly one of the previous ring's circles. What is the radius of the hole in the middle of the arrangement? What proportion of the area of the large circle is covered by the smaller circles? For this problem, getting a sufficiently good decimal approximation of the answers is fine.

Settlers of Catan A board game is played on a hexagonal grid of 19 tiles. A 'traveler' token starts on the center tile. Each turn a die is rolled to determine what neighboring tile the traveler moves to (all six directions equally likely). The turn that the traveler leaves the board, the game ends. What is the expected number of turns of the game?

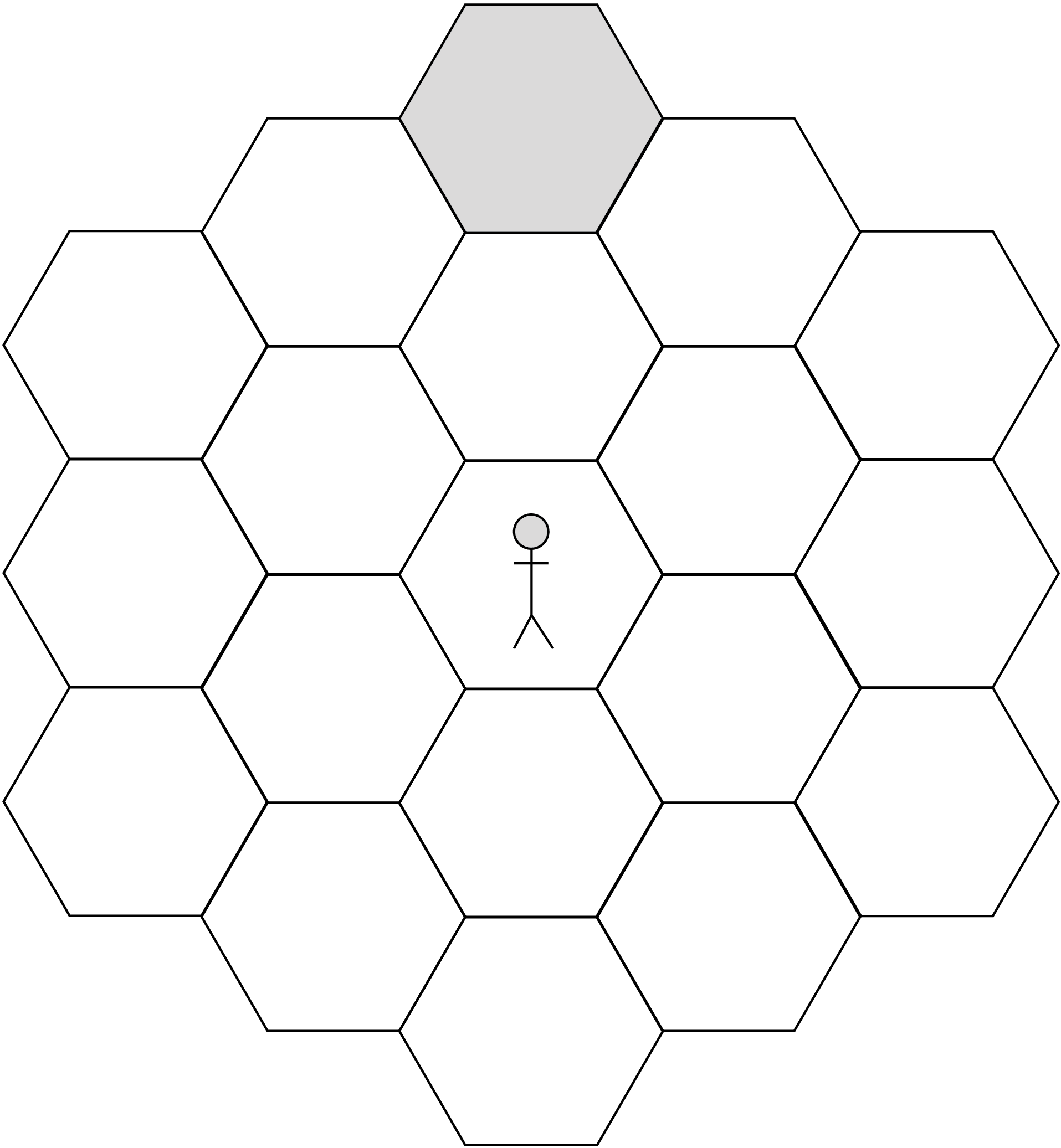Say we know that today's game ended when the traveler exited the 'northernmost' hex of the board shaded in the picture. What is the expected number of turns in the game conditioning on that fact?

Baby Wesley reads books very quickly! This is largely because whatever page he is on, say page k, of an N-page book, he selects the next page to visit uniformly randomly out of the remaining pages (so probability 1/(N-k) each for the next page to be page k+1, k+2, ..., N). He does this consistently until he finishes the book by reaching the final (Nth) page. He just picked up a book with 26 pages to read (so he's currently on 'page 0'), and his favorite picture of a monkey is on page 13. What's the probability he visits this page during this reading?

What is the probability that Wesley never flips only one page (that is never visits consecutive pages, including not visiting page 1 after starting at 'page 0') as he goes through the entire 26 page book? What happens to this probability as the length of the book N gets larger and larger?